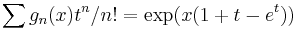Mahler polynomial

In mathematics, the Mahler polynomials g_n(x) are polynomials introduced by Mahler (1930) in his work on the zeros of the incomplete gamma function.

Mahler polynomials are given by the generating function

$\displaystyle \sum g_n(x)t^n/n! = \exp(x(1%2Bt-e^t))$

Mahler polynomials can be given as the Sheffer sequence for the functional inverse of 1+t–e^t (Roman 1984, 4.9).

References

Mahler, Kurt (1930), "Über die Nullstellen der unvollständigen Gammafunktionen." (in German), Rendiconti Palermo 54: 1–41, JFM 56.0310.01
Roman, Steven (1984), The umbral calculus, Pure and Applied Mathematics, 111, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-594380-2, MR 741185, http://books.google.com/books?id=JpHjkhFLfpgC Reprinted by Dover, 2005